​ MDP（Markov Decision Processes）是强化学习的基础，理解MDP对RL的后续学习起着关键的作用。下面利用上一个笔记的基本概念和马尔科夫性，对MDP进行展开和理解。

马尔科夫过程（Markov Process）

现实世界是复杂的，为了刻画现实中的不确定性，常引用随机的概念。在考察含有随机因素的动态系统时，常有：系统在每个时期的状态是随机的，从这个时期到下一个时期的状态按照一定概率进行转移（即状态转移概率），并且下个时期的状态只取决于这个时期的状态和转移概率，与以前状态无关。这就是前面所讲到的’马尔科夫性’。含有这种性质的离散时间的随机转移过程称为马尔科夫过程，又称马尔科夫链。

以健康和疾病为例，假设在某统计中，一个人今年健康的概率下年保持健康的概率为0.8，生病的概率为0.2。今年生病下年恢复健康的概率为0.3，继续生病的概率则为0.7。相关的状态转移过程如图(“1”代表健康，“2”代表生病)：

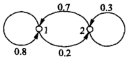
这就是一个马尔科夫过程，并且是无限循环、没有结束状态的，这种马尔科夫链称为正则链。如果有结束状态（比如死亡）则称为吸收链。

综上，对于马尔可夫过程可以用一个元组<S,P>表示，S为状态集，P为状态转移矩阵（也就是方程组中的状态转移概率组成的矩阵）：

马尔科夫决策过程（MDP）

一个基本的MDP可以用元组<S,A,R,P,γ>表示。可以看到，与马尔科夫过程相比，MDP多了A、R和γ。A表示动作集，是一个个体采取的动作；R是下一个时刻获得的奖励的数学期望：

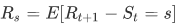
γ是衰减因子，作用于奖励R，取值区间为[0,1]。为什么要引入这么一个东西呢？其一是方便数学上的分析和处理，其二是γ的高次方趋近于0，可避免上面讲到的无限循环（计算机无法实现），另外对于人类来说未来太久远，不确定性太大。

为了评价MDP我们设计相对应的指标：

收获Return

上面讲到了奖励，所以一个状态的好坏应该可以用未来回报的期望来表示。这个值称为收获（Return）：

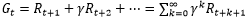
根据这个公式，可以看出时间越久就越久影响就越小。

价值函数value function

但是收获需要等到整个过程结束，否则就无法计算，所以需要再引入另外的概念，对收获的期望进行评估，这个概念就是价值函数：

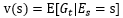
可能你会问这里不还是求return吗，只是变成了期望而已呀？！这时候神奇的东西来了，对上面的式子进行变换，运用所谓Bellman方程：

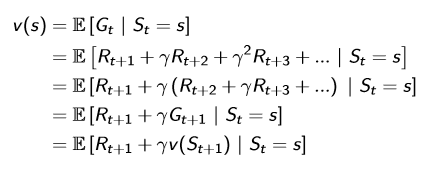
可以看到当前状态表示成下一个状态的函数！这就是Bellman的神奇之处，利用这种特性可以找到最优的价值函数。

动作-价值函数action-value function

上面提到的价值函数表征的是一个状态，在MDP里面个体还能进行决策采取动作，自然地能不能对动作也设置一个价值函数呢？答案是肯定的，这个函数就是动作-价值函数：

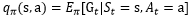
有了价值函数和动作-价值函数，我们取从一个状态转移到下一个状态进行分析。

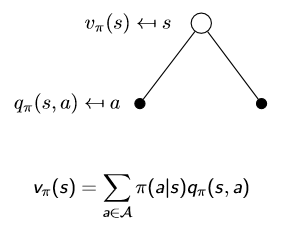
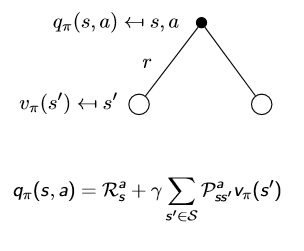
第一张图片为个体采取行动，第二张表示采取某动作后再转移到下一个状态的概率（原因是环境的影响）。把两张图结合在一起，价值函数和动作价值函数可以变为自举的形式：

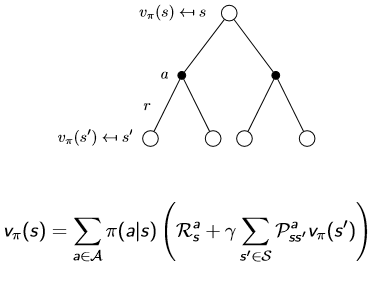
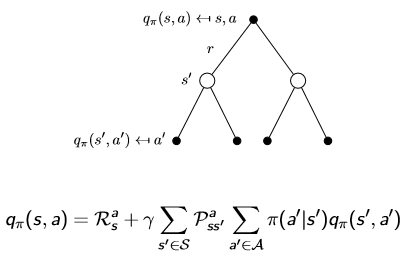
其实这两个就是Bellman方程，使状态价值和动作-价值函数的求解更加方便。关于这个方程还有Bellman期望方程和Bellman最优方程，在后续的学习中我们将体会到Bellman方程的重要性。